문제 내용
https://www.acmicpc.net/problem/1005
1005번: ACM Craft
첫째 줄에는 테스트케이스의 개수 T가 주어진다. 각 테스트 케이스는 다음과 같이 주어진다. 첫째 줄에 건물의 개수 N과 건물간의 건설순서 규칙의 총 개수 K이 주어진다. (건물의 번호는 1번부
www.acmicpc.net
서기 2012년! 드디어 2년간 수많은 국민들을 기다리게 한 게임 ACM Craft (Association of Construction Manager Craft)가 발매되었다.
이 게임은 지금까지 나온 게임들과는 다르게 ACM크래프트는 다이나믹한 게임 진행을 위해 건물을 짓는 순서가 정해져 있지 않다. 즉, 첫 번째 게임과 두 번째 게임이 건물을 짓는 순서가 다를 수도 있다. 매 게임시작 시 건물을 짓는 순서가 주어진다. 또한 모든 건물은 각각 건설을 시작하여 완성이 될 때까지 Delay가 존재한다.
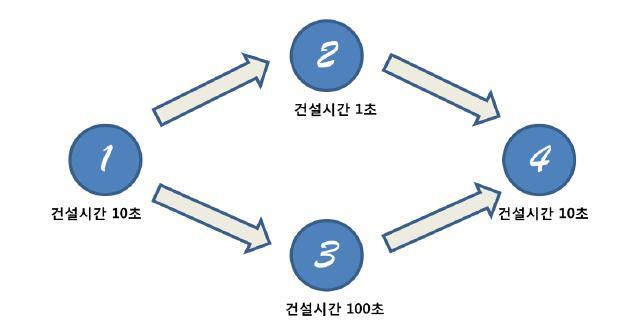
위의 예시를 보자.
이번 게임에서는 다음과 같이 건설 순서 규칙이 주어졌다. 1번 건물의 건설이 완료된다면 2번과 3번의 건설을 시작할수 있다. (동시에 진행이 가능하다) 그리고 4번 건물을 짓기 위해서는 2번과 3번 건물이 모두 건설 완료되어야지만 4번건물의 건설을 시작할수 있다.
따라서 4번건물의 건설을 완료하기 위해서는 우선 처음 1번 건물을 건설하는데 10초가 소요된다. 그리고 2번 건물과 3번 건물을 동시에 건설하기 시작하면 2번은 1초뒤에 건설이 완료되지만 아직 3번 건물이 완료되지 않았으므로 4번 건물을 건설할 수 없다. 3번 건물이 완성되고 나면 그때 4번 건물을 지을수 있으므로 4번 건물이 완성되기까지는 총 120초가 소요된다.
프로게이머 최백준은 애인과의 데이트 비용을 마련하기 위해 서강대학교배 ACM크래프트 대회에 참가했다! 최백준은 화려한 컨트롤 실력을 가지고 있기 때문에 모든 경기에서 특정 건물만 짓는다면 무조건 게임에서 이길 수 있다. 그러나 매 게임마다 특정건물을 짓기 위한 순서가 달라지므로 최백준은 좌절하고 있었다. 백준이를 위해 특정건물을 가장 빨리 지을 때까지 걸리는 최소시간을 알아내는 프로그램을 작성해주자.
입력
첫째 줄에는 테스트케이스의 개수 T가 주어진다. 각 테스트 케이스는 다음과 같이 주어진다. 첫째 줄에 건물의 개수 N과 건물간의 건설순서 규칙의 총 개수 K이 주어진다. (건물의 번호는 1번부터 N번까지 존재한다)
둘째 줄에는 각 건물당 건설에 걸리는 시간 D1, D2, ..., DN이 공백을 사이로 주어진다. 셋째 줄부터 K+2줄까지 건설순서 X Y가 주어진다. (이는 건물 X를 지은 다음에 건물 Y를 짓는 것이 가능하다는 의미이다)
마지막 줄에는 백준이가 승리하기 위해 건설해야 할 건물의 번호 W가 주어진다.
출력
건물 W를 건설완료 하는데 드는 최소 시간을 출력한다. 편의상 건물을 짓는 명령을 내리는 데는 시간이 소요되지 않는다고 가정한다.
건설순서는 모든 건물이 건설 가능하도록 주어진다.
제한
- 2 ≤ N ≤ 1000
- 1 ≤ K ≤ 100,000
- 1 ≤ X, Y, W ≤ N
- 0 ≤ Di ≤ 100,000, Di는 정수
문제 접근 방법
일단 이번 문제는 그래프로 주어지고, 간선의 방향성이 있으며 사이클이 없기 때문에 위상정렬로 풀 수 있는 문제이다.
또한 문제에서 건물마다 건물을 짓는데 걸리는 시간에 딜레이가 있다고 했다.
이말은 현재 건물과 간선으로 이어진 이전 건물들을 모두 완공해야지만 현재 건물을 건설할 수 있다는 말이고,
다르게 말하면 진입차수가 0이되는 건물들만 건설할 수 있다는 말이면서 건설의 순서가 정해져 있다는 말이다..
(사실 위상정렬 문제를 처음 풀기때문에 이외의 조건은 잘모르겠다.)
일단 로직을 보기전에 편의상 건물 = 정점 , 건물을 짓는 규칙 = 간선 으로 생각하고 말하겠다.
이번 문제를 풀기위해 필요하다고 생각하는 로직들만 정리해보겠다.
(그리고 기본적인 위상정렬을 모른다면 링크를 참고하자. https://gmlwjd9405.github.io/2018/08/27/algorithm-topological-sort.html )
로직
- 배열 정의 및 간선 표시
각 정점이 건물을 짓는데 걸리는 시간을 나타내줄 time 배열
각각의 정점가 갖고 있는 진입차수를 나타내줄 indegree 배열
n번 정점까지 건물을 완공하는 시간을 저장해줄 dp 배열
간선을 표시해주는 인접리스트가 필요하다.
더보기배열 정의 및 간선 표시
static int[] time; //각 정점의 건설시간 static int[] indegree; //각 정점의 진입차수의 개수 static int[] dp; //각 정점까지 걸리는 건설시간 static ArrayList<ArrayList<Integer>> list; //간선표시 - 입력값 및 배열 초기화 작업
당연한 말이겠지만 문제에서 주어지는 입력값과 배열을 초기화하는 작업이 필요하다.더보기초기화
T = Integer.parseInt(br.readLine()); for(int i=0; i<T; i++) { StringTokenizer st = new StringTokenizer(br.readLine()); n = Integer.parseInt(st.nextToken()); k = Integer.parseInt(st.nextToken()); dp = new int[n+1]; st = new StringTokenizer(br.readLine()); time = new int[n+1]; for(int t=1; t<=n; t++) { time[t] = Integer.parseInt(st.nextToken()); dp[t] = Integer.MIN_VALUE; } list = new ArrayList<ArrayList<Integer>>(); for(int l=0; l<=n; l++) list.add(new ArrayList<Integer>()); indegree = new int[n+1]; for(int j=0; j<k; j++) { st = new StringTokenizer(br.readLine()); int v1 = Integer.parseInt(st.nextToken()); int v2 = Integer.parseInt(st.nextToken()); list.get(v1).add(v2); indegree[v2]++; } w = Integer.parseInt(br.readLine()); //타겟 정점 - 위상 정렬 시키기
1~2번 작업을 하고나면 이제 위상정렬을 시키면서 w 정점까지 건설하는데 걸리는 시간을 구하면된다.
이때 만약 w 정점의 진입차수가 0이라면 시작정점 이기때문에 time[w] 값으로 답을 구할 수 있다.
그외의 경우를 보자.
- 큐 정의
이 로직에선 큐를 통해 정렬을 하기 때문에 큐를 정의해준다.
다만 큐의 제네릭에 대해선 이전 정점과, 현재 정점을 알려줄 수 있는 객체를 넣어야한다.
이는 후에 설명하겠지만 이전 정점까지 건물짓는데 걸리는시간을 이용해 현재 정점에서 건물짓는데 걸리는 시간을 구하기 위함이다.
static Queue<Node1005> q; //이전,현재 정점 넣어줄 큐 static class Node1005{ //이전,현재 정점 나타내는 클래스 int preV;//이전 int curV;//현재 public Node1005(int preV, int curV) { this.preV = preV; this.curV = curV; } } - 시작정점 추가 및 addCnt변수 선언
큐를 돌리기전에 시작정점을 추가하여 어디서부터 건설을 시작할지 문제의 조건에 따라 나뉘게된다.
이때 시작 정점은 진입차수가 0인것들로 판단해낼 수 있다.
또한 addCnt 변수는 현재 큐에 추가된 정점의 개수를 나타내고 이를 선언한 이유는
큐에 들어있는 정점들이 각각 건설을 동시에 진행할 수 있기 때문에
addCnt를 갱신하면서 큐에 들어있는 정점의 개수만큼만 끊어서 위상정렬을 실행하기 위해서 선언했다.
public static void topologicalSort() { q = new LinkedList<Node1005>(); /* * 하나의 정점에대해 인접한 정점(진입차수가 0인것만)의 개수를 세고 * 그 개수만큼 끊어서 반복문을 돌리기 위해서(동시에 실행되는거 고려) * addCnt변수 선언 */ int addCnt = 0; //시작정점들 탐색 -> 진입차수가 0인 것들 for(int i=1; i<=n; i++) { if(indegree[i]==0) { addCnt++; q.add(new Node1005(0, i)); } } while(!q.isEmpty()) { //sectionSort를 통해 addCnt개수 만큼 끊어서 위상정렬 시작 if(addCnt!=-1) addCnt = sectionSort(addCnt); else return; } } - dp값 채우고 addCnt갱신
addCnt의 개수 만큼 q에서 정점하나씩 빼면서 dp의 값을 채우는 작업을 한다.
첫번째로 dp값을 채우는 식의 정의는 기본적으로 다음과 같이 할 수 있다.
현재 정점까지 걸리는시간 = Math.max( 이전 정점까지 걸리는시간+현재정점 건설시간, 현재 정점까지 걸리는시간) 즉,
dp[현재 정점] = Math.max( dp[이전정점] + time[현재정점] , dp[현재정점] ) 으로 정의 할 수 있다.
두번째로 고려해야 할것은 dp값을 채울때 진입차수가 2개 이상인것들을 채우는 것이다.
예를들어 5,6번 정점이 7번 정점 방향으로 간선이 있을때 dp[5] = 15 , dp[6] = 10, time[7] = 5 라고하자.
그럼 우리는 dp[7]을 구하기 위해서 dp[5]+time[7] , dp[6]+time[7]을 비교해야 한다.
근데 만약 큐에 정점이 (5,6)의 순서로 돼있다면 어떻게 될까.
5번정점이 돌고나면 큐에 있는 6이라는 정점이 때문에 7번 정점은 진입차수가 1이 되고 큐에 추가되지 않는다.
6번정점이 돌고나면 7번정점은 진입차수가 0이기 때문에 큐에 추가된다.
그리고 7번정점을 돌때 가장 최근정점(바로전 정점)이 6번 정점이기 때문에
dp[7] = Math.max( dp[6] + time[7] , dp[7] ) 하나만 비교하게 된다.
즉, dp[5]+time[7]은 비교할 수가 없다.
그래서 dp[7] = 20 이아닌 15가 나오게 된다.
이를 해결하기 위해 진입차수가 0이 아닐때 dp값을 미리 채워줘야 한다.
즉, dp[5]+time[7] 과 dp[6]+time[7]을 비교하기 위해 먼저 dp[5]+time[7]을 dp[7]을 아래코드 처럼 해줘야한다.
dp[다음 정점] = Math.max( dp[현재 정점]+time[다음 정점] , dp[다음 정점] )
마지막으로 addCnt를 갱신해 준다.
작업 순서에따라 큐에 추가된 정점을 돌았을때 그 정점들에 인접한 정점들도 동시에 건설을 할수 있기때문에
큐에 추가된 정점만큼 addCnt를 다시 갱신한다.
public static int sectionSort(int addCnt) { int cnt = 0; //큐에 드가는 정점 개수세는 변수(진입차수 0이되는 것들) //addCnt개수만큼 돌리기 for(int i=0; i<addCnt; i++) { Node1005 v = q.poll(); //현재 정점이 타겟과 같으면 dp배열 갱신 후 -1 반환. if(v.curV==w) { //현재 정점까지 걸리는 시간 = Math.max(이전 정점까지 걸리는시간+현재 정점의 건설시간 , 현재 정점까지 걸리는 시간) dp[v.curV] = Math.max(dp[v.preV]+time[v.curV], dp[v.curV]); return -1; } dp[v.curV] = Math.max(dp[v.preV]+time[v.curV], dp[v.curV]); //현재 정점에 인접한 노드를 탐색 for(int j=0; j<list.get(v.curV).size(); j++) { int nextV = list.get(v.curV).get(j); indegree[nextV]--;//현재 정점을 탐색했기때문에 인접노드의 진입차수 하나 감소 //인접노드가 진입차수가 0이될때 큐에 추가, cnt 증가 if(indegree[nextV]==0) { q.add(new Node1005(v.curV, nextV)); cnt++; }else { /* * 인접한 정점의 진입차수가 0이 아니라는 말은 다른 정점들에서 * 인접한 정점으로 간선이 있다는 말이다. * 따라서 인접한 정점으로 진입하는 모든 정점들의 건설시간을 고려해야한다(동시진행때문) * 이를 고려하기 위해 진입차수가 0이 아닐땐 미리 인접한 정점이 건물짓는데 걸리는 시간을 * 넣어놔야한다. * * 예를 들어 5,6번 정점이 7번 정점방향으로 간선이 있고, * dp[5]=20 , dp[6]=10 , time[7]=5 일때 * dp[7]=25가 나와야한다. * 이때, 만약 큐에 (5,6)의 순서대로 있다면 * 5번정점에서 7번정점으로 갔을때 걸리는 시간인 25와 * 6번정점에서 7번정점으로 갔을때 걸리는 시간인 15를 비교해야 하는데 * 아래 코드가 없다면 7번 정점은 6번정점이 탐색을 마친 후 큐에 추가가 된다. * 그래서 dp[7]은 6번정점에서 7번정점으로 갔을때 걸리는 시간밖에 알수가 없다. * 즉, dp[7]이 15일때와 25일때를 비교해주기 위해 필요한 코드이다. */ dp[nextV] = Math.max(dp[v.curV]+time[nextV], dp[nextV]); } } } return cnt; //큐에추가된 노드 개수만큼 반환. } - 목표 정점에서 걸리는 시간 출력
위의 과정을 통해 dp배열을 채우고 나면 dp[w]를 통해 목표 정점까지 걸리는 시간을 알아낼 수 있다.
- 큐 정의
아래에서 자세한 코드를 보자.
풀이
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
public class Main {
static int T, n, k, w; //테케, 정점, 간선, 타겟정점
static int[] time; //각 정점의 건설시간
static int[] indegree; //각 정점의 진입차수의 개수
static int[] dp; //각 정점까지 걸리는 건설시간
static ArrayList<ArrayList<Integer>> list; //간선표시
static Queue<Node1005> q; //이전,현재 정점 넣어줄 큐
static class Node1005{ //이전,현재 정점 나타내는 클래스
int preV;//이전
int curV;//현재
public Node1005(int preV, int curV) {
this.preV = preV;
this.curV = curV;
}
}
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
/*--------------------------변수값 할당 및 초기화-------------------------------------*/
T = Integer.parseInt(br.readLine());
for(int i=0; i<T; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
k = Integer.parseInt(st.nextToken());
dp = new int[n+1];
st = new StringTokenizer(br.readLine());
time = new int[n+1];
for(int t=1; t<=n; t++) {
time[t] = Integer.parseInt(st.nextToken());
dp[t] = Integer.MIN_VALUE;
}
list = new ArrayList<ArrayList<Integer>>();
for(int l=0; l<=n; l++)
list.add(new ArrayList<Integer>());
indegree = new int[n+1];
for(int j=0; j<k; j++) {
st = new StringTokenizer(br.readLine());
int v1 = Integer.parseInt(st.nextToken());
int v2 = Integer.parseInt(st.nextToken());
list.get(v1).add(v2);
indegree[v2]++;
}
w = Integer.parseInt(br.readLine()); //타겟 정점
/*--------------------------------------------------------------------*/
if(indegree[w]==0) {//타겟 정점이 시작 정점일때
sb.append(time[w]).append("\n");
continue;
}
topologicalSort();//위상정렬
sb.append(dp[w]).append("\n");
}
System.out.println(sb.toString());//출력
}
//위상정렬
public static void topologicalSort() {
q = new LinkedList<Node1005>();
/*
* 하나의 정점에대해 인접한 정점(진입차수가 0인것만)의 개수를 세고
* 그 개수만큼 끊어서 반복문을 돌리기 위해서(동시에 실행되는거 고려)
* addCnt변수 선언
*/
int addCnt = 0;
//시작정점들 탐색 -> 진입차수가 0인 것들
for(int i=1; i<=n; i++) {
if(indegree[i]==0) {
addCnt++;
q.add(new Node1005(0, i));
}
}
while(!q.isEmpty()) {
//sectionSort를 통해 addCnt개수 만큼 끊어서 위상정렬 시작
if(addCnt!=-1) addCnt = sectionSort(addCnt);
else return;
}
}
public static int sectionSort(int addCnt) {
int cnt = 0; //큐에 드가는 정점 개수세는 변수(진입차수 0이되는 것들)
//addCnt개수만큼 돌리기
for(int i=0; i<addCnt; i++) {
Node1005 v = q.poll();
//현재 정점이 타겟과 같으면 dp배열 갱신 후 -1 반환.
if(v.curV==w) {
//현재 정점까지 걸리는 시간 = Math.max(이전 정점까지 걸리는시간+현재 정점의 건설시간 , 현재 정점까지 걸리는 시간)
dp[v.curV] = Math.max(dp[v.preV]+time[v.curV], dp[v.curV]);
return -1;
}
dp[v.curV] = Math.max(dp[v.preV]+time[v.curV], dp[v.curV]);
//현재 정점에 인접한 노드를 탐색
for(int j=0; j<list.get(v.curV).size(); j++) {
int nextV = list.get(v.curV).get(j);
indegree[nextV]--;//현재 정점을 탐색했기때문에 인접노드의 진입차수 하나 감소
//인접노드가 진입차수가 0이될때 큐에 추가, cnt 증가
if(indegree[nextV]==0) {
q.add(new Node1005(v.curV, nextV));
cnt++;
}else {
/*
* 인접한 정점의 진입차수가 0이 아니라는 말은 다른 정점들에서
* 인접한 정점으로 간선이 있다는 말이다.
* 따라서 인접한 정점으로 진입하는 모든 정점들의 건설시간을 고려해야한다(동시진행때문)
* 이를 고려하기 위해 진입차수가 0이 아닐땐 미리 인접한 정점이 건물짓는데 걸리는 시간을
* 넣어놔야한다.
*
* 예를 들어 5,6번 정점이 7번 정점방향으로 간선이 있고,
* dp[5]=20 , dp[6]=10 , time[7]=5 일때
* dp[7]=25가 나와야한다.
* 이때, 만약 큐에 (5,6)의 순서대로 있다면
* 5번정점에서 7번정점으로 갔을때 걸리는 시간인 25와
* 6번정점에서 7번정점으로 갔을때 걸리는 시간인 15를 비교해야 하는데
* 아래 코드가 없다면 7번 정점은 6번정점이 탐색을 마친 후 큐에 추가가 된다.
* 그래서 dp[7]은 6번정점에서 7번정점으로 갔을때 걸리는 시간밖에 알수가 없다.
* 즉, dp[7]이 15일때와 25일때를 비교해주기 위해 필요한 코드이다.
*/
dp[nextV] = Math.max(dp[v.curV]+time[nextV], dp[nextV]);
}
}
}
return cnt; //큐에추가된 노드 개수만큼 반환.
}
}마치며
처음 풀어본 위상정렬 문제이다. 작업순서와 방향성이 있고 사이클이 없는 그래프일때 사용할 수 있는 알고리즘이고 이알고리즘은 모든 노드를 확인하는데 O(V) , 간선을 제거하는데 O(E)
즉 O(V+E)의 시간복잡도를 갖게된다.
'알고리즘 > BOJ' 카테고리의 다른 글
| [JAVA] BOJ(백준) - 연구소 - 14502 (0) | 2022.02.16 |
|---|---|
| [JAVA] BOJ(백준) - 가르침 - 1062 (0) | 2022.02.15 |
| [JAVA] BOJ(백준) - 파티 - 1238 (0) | 2022.02.08 |
| [JAVA] BOJ(백준) - 빗물 -14719 (0) | 2022.02.06 |
| [JAVA] BOJ(백준) - 네트워크 연결 - 1922 (0) | 2022.02.02 |
