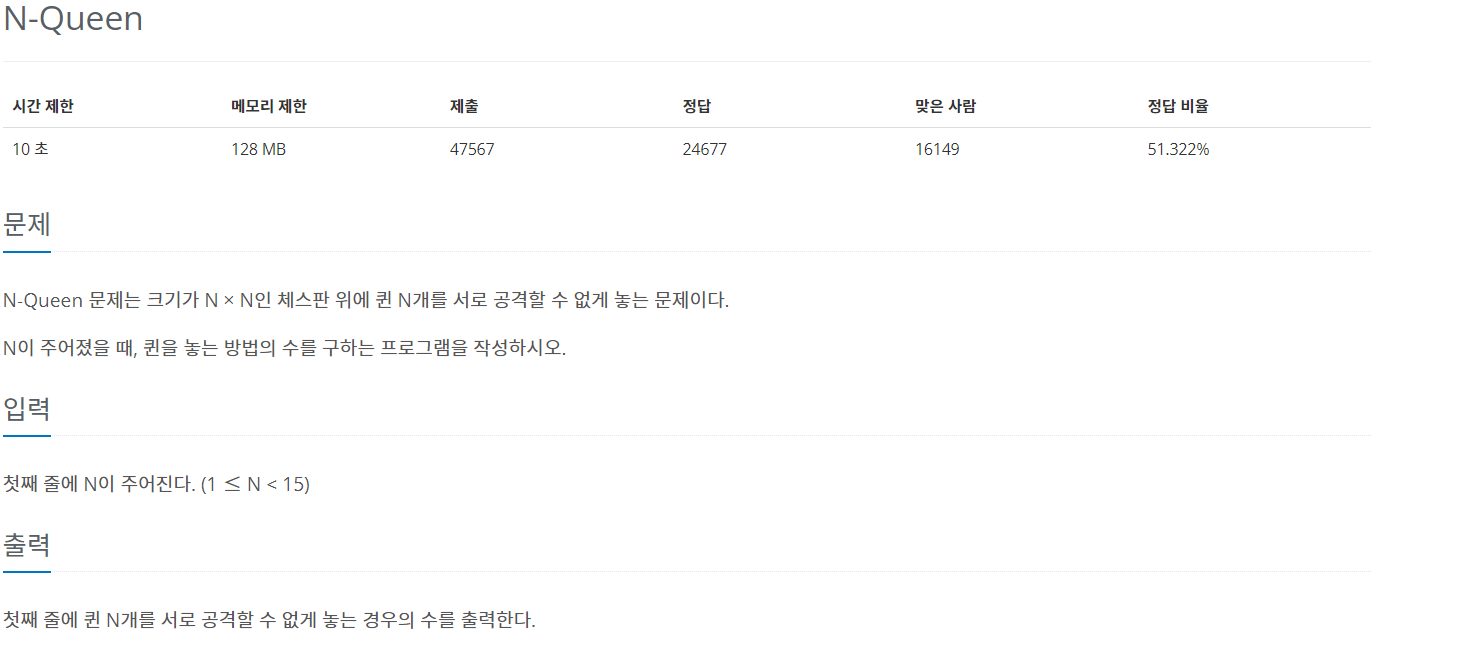
- 문제내용

- 문제 접근 방법
문제 자체는 N을 입력 받았을때 N*N 체스판에다 N개의 퀸을 서로 공격 못하는 위치에 올려 놓을수 있는 경우의 수를 구하면 되는 문제이다. 이 방법도 전에했던 N과 M(1) 문제처럼 백트래킹으로 풀면되는데 가장먼저 고려해야 했던것들이 있다.
- 퀸은 상,하,좌,우,대각선 방향으로 끝에서 끝까지 공격 범위이다.
- 상,하,좌,우에 대해선 퀸은 무조건 체스판에서 하나의 행이나 하나의 열에 한개밖에 못놓는다. 즉, 행과 열마다 겹치는 퀸이 있으면 안된다.
- 이부분이 가장 어려웠는데,, 체스판에서 대각선 방향도 겹치는 퀸이 있어선 안된다.
쓰고보니 결국 다 같은 말같은데 음,., 저 조건을 고려해야 필요없는 경우의 수를 줄일수 있다. 처음엔 체스판을 2차원 배열로 만들어서 하나하나의 경우의 수를 다 따지려고 했는데 대가리 빠개질꺼 같아서 포기하고 다른 방법을 생각해봤다. 그래서 결국
열(세로)에 대한 방문여부를 알수 있는 배열 1개.
좌상단-우하단(대각선)에 대한 퀸의 점유 상황을 알려주는 배열 1개.
좌하단-우상단(대각선)에 대한 퀸의 점유 상황을 알려주는 배열 1개.
3개의 경우를 알면 겹치지 안는곳 즉, false가 되는 부분이 퀸이 놓일수 있는 경우가 된다. 2차원 배열로 일일히 체크를 안해도 된다.
중요하게 생각해야 하는점은 4*4 체스판에서 예를들어
좌상단-우하단의 경우 (0,0)에 퀸이 있으면 (1,1), (2,2), (3,3) 은 모두 같은 자리에 위치해 있다고 가정하는 것이다.
이때 행이 x, 열이 y라고 했을 때 모두 x-y의 값이 같은 것을 알수있다.
좌하단-우상단의 경우 (3,0)에 퀸이 있으면 (2,1), (1,2), (0,3) 도 마찬가지다.
이때는 x+y의 값이 같은 것을 알수있다.
이를 이용한 코드 풀이를 아래서 보자~
import java.util.*;
// 대각선 / -> x+y 가 같은것들은 같은위치
// 대각선 \ -> x-y 가 같은것들은 같은위치
public class BOJ_9663 {
static int N;
static boolean[] sero; //0~N열까지 퀸이 놓였는지 알기위한 배열
static boolean[] diagonal1; //좌상단 - 우하단 점유상황 배열
static boolean[] diagonal2; //좌하단 - 우상단 점유상황 배열
static int answer=0;
public void chespan(int N,int depth) {
//종료조건
if(depth == N) { //행이 N과 같아지면 퀸이 다 배치된것.
answer++;
return;
}
for(int i=0; i<N; i++) { //N*N 체스판이고 열이나 행 하나에 퀸하나만 놓이므로 N까지 돌면됨.
//i번째 열 or 좌상단-우하단 대각 or 좌하단-우상단 대각에 퀸이 있으면 퀸을 놓을수 없으므로 continue
if(sero[i] || diagonal1[depth-i+N-1] || diagonal2[depth+i]) {continue;}
//퀸을 놓으면 아래의 상황 전부 true 처리
sero[i]=true;
diagonal1[depth-i+N-1]=true;
diagonal2[depth+i]=true;
chespan(N,depth+1); // 재귀호출
//재귀 호출이 끝나면 다시 false 처리
sero[i]=false;
diagonal1[depth-i+N-1]=false;
diagonal2[depth+i]=false;
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
sc.close();
//N*N행렬일때 대각선의 개수는 N*2-1이됨.
diagonal1 = new boolean[(N*2)-1];
diagonal2 = new boolean[(N*2)-1];
sero = new boolean[N];
new BOJ_9663().chespan(N,0);
System.out.println(answer);
}
}
코드에서 depth는 행이라고 생각하고 풀었다. 대각선의 경우 x+y는 depth+i 로 그냥 처리해도 되지만 x-y는 인덱스를 음수로 보내면 안되기 때문에 x-y+N-1 즉, depth-i+N-1 로 바꿔서 처리했다.
- 마치며
대각선의 인덱스를 확인하는 방법(x-y+N-1)은 유튜브를 참조해서 풀수 있었다. 도대체 저런 생각은 어떻게 해내는 걸까 ㅋㅋㅋㅋㅋㅋㅋ 다같이 공부 열심히 합시다!
'알고리즘 > BOJ' 카테고리의 다른 글
| [JAVA]BOJ(백준) - 바이러스 - 2606 (0) | 2021.10.08 |
|---|---|
| [JAVA]BOJ[백준] - DFS와 BFS - 1260 (0) | 2021.10.07 |
| [JAVA] BOJ(백준) - N과 M(2) - 15650 (0) | 2021.10.01 |
| [JAVA]BOJ(백준) - 연산자 끼워넣기 - 14888 (0) | 2021.10.01 |
| [JAVA] BOJ(백준) - N과 M(1) - 15649 (0) | 2021.09.28 |



